¿Cuál es el inverso de un número? ¿Es lo mismo que calcular su opuesto? Usa nuestra calculadora online y obtén el inverso de cualquier cantidad de forma inmediata. Sólo tienes que escribir el número del cual quieres calcular su opuesto, presionar el botón de calcular y automáticamente obtendrás el resultado en pantalla.
Si quieres saber más sobre cuál es el inverso de un número y cómo se calcula, sigue leyendo.
Contenido de este artículo
¿Qué es el inverso de un número?
El inverso de un número es igual a otro número que obtenemos al resolver la operación 1/x, siendo x el número inicial.
No debe confundirse el inverso de un número con su opuesto. Mientras que el inverso es 1/x, el opuesto es igual a -x. Es decir, el inverso de 2 es igual a 1/2 mientras que su opuesto será igual a -2.
Para diferenciar ambos conceptos, a continuación os dejamos con un par de "trucos" o reglas que nos ayudarán a recordar la diferencia entre el opuesto y el inverso de un número:
- El inverso de un número multiplicado por el número nos da 1 como resultado. Ejemplo:
3 x 1/3 = 1
- El opuesto de un número sumado con el propio número nos da 0 como resultado. Ejemplo:
3 + (-3) = 0
Cómo calcular el inverso de un número
Como ya hemos visto en el punto anterior, el inverso de un número x se calcula mediante la fórmula 1/x. Para que quede claro, a continuación vamos a ver algunos ejemplos del cálculo de números inversos:
| Número (x) | Inverso (1/x) | Opuesto (-x) |
|---|---|---|
| 2 | 1/2 =0,5 | -2 |
| 3 | 1/3 = 0,33 | -3 |
| 5 | 1/5 = 0,2 | -5 |
| -5 | 1/-5 = -0,2 | 5 |
Como puedes ver, la operación es sencilla y no entraña ningún tipo de dificultad. Si el número es negativo se calcula exactamente igual.
¿Cuál es el inverso de 0?
El inverso de cero no existe. ¿Por qué? Esto se debe a que cualquier número dividido entre cero nos da lugar a una indeterminación cuyo valor es infinito.
1/0 = ∞
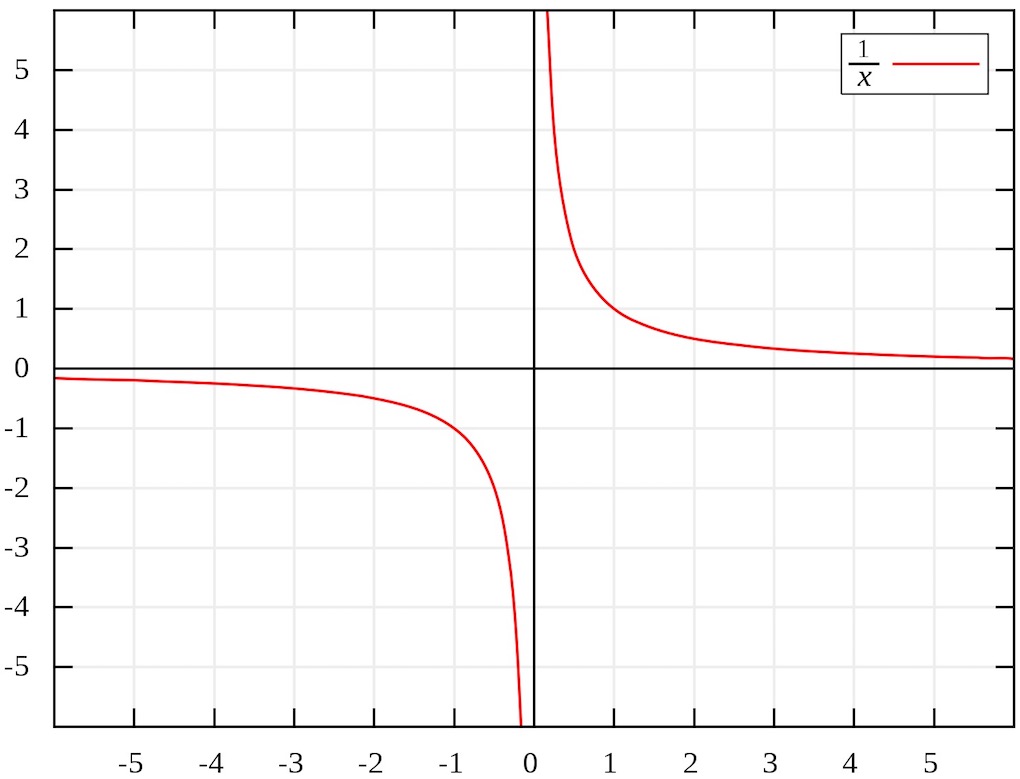
Para que se entienda mejor, en la gráfica que tenéis encima de estas líneas podéis ver una representación de lo que sucede cuando intentamos calcular el inverso de cero por la izquierda y por la derecha, obteniendo como resultado que la inversa vale -∞ y +∞ respectivamente.
Por todo esto, podemos ver algunas propiedades de la función inversa:
- No está definida cuando x = 0
- Para valores de x mayores que 0 (x > 0), la función toma valores positivos. A medida que aumentamos el valor de x, la función se va aproximando a cero.
- Para valores de x menores que 0 (x < 0), la función toma valores negativos. Si nos vamos aproximando a valores negativos cada vez más próximos a -∞, la función va acercándose a valer cero.
- Se trata de una función simétrica con respecto al origen y con respecto a la bisectriz que recurre el segundo y cuarto cuadrante.
- El inverso del inverso es el mismo número. Por ejemplo, si queremos calcular el inverso del inverso de 9, tenemos que:
1/1/9 = 9
Cómo calcular el inverso de un número con la calculadora
Si tienes una calculadora científica cerca, puedes calcular el inverso de un número de forma sencilla. Sólo tienes que localizar la tecla que tiene grabado "x-1" (la que te hemos recuadrado en rojo en la foto de arriba).
Si tu calculadora tiene dicha tecla, podrás hacer la función inversa de cualquier número de forma mucho más cómoda. Por ejemplo, si queremos calcular el inverso de 8, la secuencia de teclas a pulsar será la siguiente:
8 → x-1 → =
Fracción inversa
Si nos piden calcular la inversa de una fracción, simplemente tenemos que darla la vuelta, es decir:
- El numerador pasa a ser el denominador
- El denominador pasa a ser el numerador
No tenemos que hacer ningún tipo de operación. Vamos a verlo con varios ejercicios resueltos:
- La fracción inversa de 4/5 es 5/4
- La fracción inversa de 4/7 es 7/4
Matriz inversa
Si lo que quieres es calcular la matriz inversa, a continuación te dejamos con las calculadoras para resolverlas en función de sus dimensiones. En cada una de esas páginas encontrarás la explicación de cómo se hace con ejemplos resueltos y más.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.


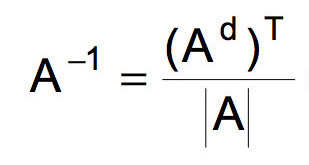
Hola
Existe alguna propiedad sobre el inverso de los números múltiplos de 2, Z4, de 4 , Z8 de 3, Z6 etc. Y si es así como se denomina?
Gracias