Calcular logaritmos online sin necesidad de calculadoras ni fórmulas es posible gracias a nuestra herramienta. Sólo tienes que introducir el valor de la base del logaritmo y el número sobre el que quieres aplicar la operación.
Recuerda que la teoría nos indica que el logaritmo de un número, en una base dada, es el exponente al cual debemos elevar la base para obtener ese mismo número. Este enunciado teórico queda recogido en la siguiente fórmula matemática:
Vista la teoría un poco por encima, ya puedes pasar a calcular el logaritmo de forma online con nuestra herramienta:
Si lo prefieres, también puedes calcular logaritmos neperianos que son aquellos en los que la base corresponde al valor del número 'e'. Por supuesto, también tenemos una sección dedicada a la operación del antilogaritmo, la operación inversa al log de un número.
Contenido de este artículo
- Cosas que debes saber de los logaritmos
- Propiedades de los logaritmos
- Ejercicios resueltos de logaritmos
- ¿Cuál es la base de un logaritmo?
- ¿Cómo resolver una ecuación con logaritmos?
- Calcular logaritmos en Excel
- ¿Para qué sirven los logaritmos?
- Cómo funciona la calculadora de logaritmos
- Cómo resolver logaritmos con la calculadora científica
Cosas que debes saber de los logaritmos
La función logaritmo, por su definición, conlleva una serie de condiciones que debemos conocer para no caer en errores de cálculo:
- No se puede calcular el logaritmo en base negativa de un número.
- No existe el logaritmo de un número negativo o el logaritmo de cero.
- El logaritmo del número 1 es igual a cero: logx1 = 0
- El logaritmo en base x del número x es igual a 1: logxx = 1
- El logaritmo en base x de una potencia en base x es igual al exponente de la potencia: logxxn = n
Propiedades de los logaritmos
Además de lo anterior, realizar operaciones con logaritmos está sujeto a una serie de propiedades que mencionamos a continuación. Cuando te enfrentes a ejercicios de logaritmos es muy importante que las tengas en cuenta ya que te pueden facilitar mucho encontrar el resultado:
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores de la multiplicación:
- El logaritmo de una división es igual a la resta de los logaritmos del dividendo menos el logaritmo del divisor:
- El logaritmo de una potencia equivale a la multiplicación del exponente por el logaritmo de la base de la potencia:
- El logaritmo de una raíz se puede expresar de la siguiente forma:
- Para realizar un cambio de base, tenemos que hacer el cociente del logaritmo del número en la nueva base entre el logaritmo de la base de partida:
Ejercicios resueltos de logaritmos
Para que entiendas bien cómo se han de resolver los logaritmos, vamos a ver algunos ejemplos bastante frecuentes.
Cuál es el logaritmo de 2
Siempre que no nos especifiquen la base del logaritmo, tomaremos como valor típico base 10. Por lo tanto, tenemos que calcular:
log(2) = x → 2 = 10x
¿Por qué número tenemos que elevar a 10 para que nos de como resultado 2? La respuesta es 0,3.
Por lo tanto, log(2) = 0,3
Cuál es el logaritmo de 50
Por si aún tenemos dudas de cómo calcular logaritmos, vamos a ver otro ejemplo en el que nos piden calcular el log de 50. De nuevo, como no especifican base tomaremos 10 como valor típico:
log(50) = x → 50 = 10x
A simple vista sabemos que x será un valor comprendido entre 1 y 2 ya que 101= 10 (nos quedamos cortos) y 102 = 100 (nos pasamos).
En este caso, la respuesta es que el log(50) = 1,70
Si tienes dudas o quieres resolver algún log en particular, escribe un comentario y te ayudaremos con el ejercicio.
¿Cuál es la base de un logaritmo?
Si nos piden calcular la base de un logaritmo, tenemos que volver de nuevo a la fórmula que vimos al principio. Vamos a verla de nuevo:
loga(b) = x → b = ax
El valor de la base del logaritmo es a, ¿pero cómo la sacamos si nos dan cuánto vale el logaritmo de un número? Para entenderlo mejor, vamos a verlo con un ejemplo práctico:
loga(8) = 3 → 8 = a3
Para sacar la base, tenemos que encontrar un número que elevado al cubo nos de 8. Esto es una operación sencilla ya que sabemos que para despejar una potencia, la operación pasa al lado contrario en forma de raíz. Es decir:
a = ∛8 = 2
Hemos calculado la raíz cúbica de 8 y el resultado es 2. Por lo tanto, la base de nuestro logaritmo es 2.
En el caso de que no haya quedado claro, vamos a ver otro ejercicio más en el que nos piden averiguar cuál es la base del logaritmo:
loga(16) = 2 → 16 = a2
En este caso, la solución es sencilla ya que sólo tendremos que calcular la raíz cuadrada de 16. Resolvemos y nos queda:
a = √16 = 4
¿Alguna duda? Pregúntanos!
¿Cómo resolver una ecuación con logaritmos?
Para resolver una ecuación con logaritmos tienes que aplicar las propiedades y la fórmula de la definición de logaritmos que hemos visto más arriba. Expresar un logaritmo como una potencia te ayudará a hacer muchos ejercicios sencillos pero para los más complicados tendrás que hacer uso también de las propiedades.
Por ejemplo, vamos a resolver la siguiente ecuación con logaritmos:
log x + log 4 = log 32
La suma de dos logaritmos se puede expresar en forma de multiplicación. Por tanto, la ecuación anterior queda de esta forma
log4x = log32
Despejamos y nos queda que:
4x = 32
x = 8
Lógicamente hay ecuaciones con logaritmos mucho más complejas de resolver y no será tan evidente su resolución como en el ejemplo anterior.
Calcular logaritmos en Excel
Si quieres crear tu propia calculadora de logaritmos usando Excel, tienes que utilizar la función LOG que te permitirá calcular logaritmos de un número en cualquier base.
Para utilizar esta fórmula, escoge una celda de tu hoja de cálculo y escribe esta función:
=LOG(A1;B2)
Debes tener en cuenta que:
- A1 es la coordenada de la celda en la que se encuentra el número para el cual quieres calcular su logaritmo.
- B2 es la base del logaritmo.
Tras escribir la fórmula para resolver logaritmos en Excel, obtendrás el cálculo automatizado para utilizarlo siempre que quieras.
¿Para qué sirven los logaritmos?
Los logaritmos nacieron como una herramienta para facilitar la resolución de ejercicios aritméticos y geométricos, evitando de esta forma tener que hacer complejas multiplicaciones y divisiones. Tal y como hemos visto antes, el logaritmo es capaz de transformar las multiplicaciones en sumas y las divisiones en restas.
Pero, ¿para qué sirven los logaritmos? No hay una respuesta única a esta pregunta porque los logaritmos sirven para múltiples ámbitos y por eso se utilizan en economía, banca, estadística, publicidad, medicina, psicología, física, ingeniería, biología, geología, astronomía, química, topografía, aviación, música y un largo etcétera.
Por esto mismo, es muy importante que sepas cómo resolver logaritmos y entender muy bien sus propiedades.
Cómo funciona la calculadora de logaritmos
En este vídeo hemos grabado cómo se utiliza nuestra calculadora de logaritmos para que no tengas ninguna duda de cómo se resuelve esta operación usando nuestra herramienta.
Para resolver logaritmos online sólo debes introducir el valor de la base e introducir el número. Después pulsa el botón de calcular para conocer el log(x).
Si aún así tienes dudas a la hora de calcular logaritmos, déjanos un comentario y trataremos de ayudarte lo antes posible. Esperamos que nuestra página para resolver logaritmos te haya servido de ayuda.
Cómo resolver logaritmos con la calculadora científica
Si tienes a mano una calculadora científica, puedes resolver logaritmos de forma muy sencilla.
Nosotros hemos tomado como ejemplo una calculadora científica de Casio pero lo cierto es que la mayoría de marcas y calculadoras simples tienen una tecla dedicada a calcular logaritmos.
La podrás identificar de forma muy sencilla ya que verás las letras "log" grabadas en su superficie por lo que sólo tendrás que pulsarla, escribir el número del cual quieres obtener su logaritmo y pulsar la tecla igual (=) para conocer el resultado.
Ten en cuenta que por defecto, la calculadora de logaritmos realiza la operación con el log en base 10 pero si necesitamos cambiarla, también podremos hacerlo sin problema.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.

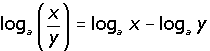

Por favor no puedo resolver una ecuacion logaritmica para hallar x y es la siguiente, agradezco infinitamente su respuesta:
2 logx=log2+log〖(3x-4)〗
Hola Luz,
No podemos resolverte el ejercicio ya que este no es nuestro propósito pero si podemos ayudarte a que consigas hacer esa ecuación logarítmica.
Lo primero que debes tener en cuenta es que tienes que despejar la x y para ello, debes tener en cuenta estad sos propiedades de los logaritmos:
Primera propiedad
log M – log N = log (M/N)
Segunda propiedad
n·log P = log Pⁿ
Aplicándolas a tu ecuación logarítmica, la puedes resolver con relativa facilidad. Si aún así tienes problemas, dinos donde te has atascado y te ayudamos.
Saludos!
Buenas tardes
Como se haría el siguiente logaritmo?
ln raíz cúbica de e
Hola Juan,
No solemos resolver los ejercicios ya que esa no es nuestra finalidad pero te voy a dar pistas para que lo resuelvas. Lo que tienes que hacer es expresar la raíz cúbica como una potencia y usar las propiedades de los logaritmos.
Entonces verás que ln(∛e) = 1/3ln(e)
Eso ya es muy fácil de resolver.
Saludos!
hola, me gustaría que me ayudasen a resolver este logaritmo(el log(x2-1) quiere decir que x esta elevado al cuadrado)
log(x+1)-log(x2-1)=log(x+√ 7)+log(x-√ 7)
Hola Mariby,
No entendemos bien el enunciado así que no podemos ayudarte. Lo siento.
Hola necesito ayuda con este logaritmo log4 (0’0625) gracias.
Hola Javi,
Lo que quieres calcular es un logaritmo en base 4 cuyo resultado es -2.
Puedes comprobarlo tú mismo resolviendo la regla básica de los logaritmos
b = ax
En este caso:
0,0625 = 4-2
NECESITO AYUDA RÁPIDO CON ESTO!!!!!!!!!!!
por favor podrían decirme como se hace?
log5 (2x+5) – log 5 (x+3)
2. log3 (x+2) = log3 729
log 2 (x-1) + log 2 (3x+1) =6
4. log x – log 9+2 =0
excelente página, trabajo claro y conciso, sin tanto término técnico inútil de adorno, muchas gracias, sigan así
Muchas gracias Daniel,
La finalidad de nuestras calculadoras es justamente esa que comentas: encontrar el resultado que buscas de forma sencilla.
Esperamos verte más pronto y si te ha quedado alguna duda sobre los logaritmos pregúntanos con total confianza que te intentaremos ayudar lo antes posible.
Saludos!
No pueden introducirse bases decimales?
Hola Sofía,
Sí se puede calcular logaritmos con base decimal pero el separador de decimales que usamos en España es la ,
El . nosotros lo utilizamos como separador de miles.
Saludos!
Saludos!
Hola. Su calculadora es realmente fantástica. Antes para resolver los logaritmos ponía en excel la base y los exponentes 1.1, 1,2, 1.3, 1.4… y realizaba la operación para dar con el exponente que cuadraba; con su calculadora lo hago en un segundo! Sólo tengo una pregunta: si quisiera resolver como resolver mecánicamente esto por ejemplo: log15X=150? como podría resolverlo
Hola Tonatiuh,
Para resolver logaritmos no queda más remedio que usar el método tradicional con la fórmula. Hay algunas bases logarítmicas como 2 o 10 que permiten resolver logaritmos de forma mental con facilidad pero otras requieren usar la fórmula o nuestra calculadora para ahorrar tiempo.
Saludos y muchas gracias por el comentario, nos alegra que te guste.
x√ 128 +2x√ 128=20
el x y el 2x son elevevados sobre la raiz ayuen con esta
Hola Francisco,
No me queda claro si tienes que calcular el logaritmo ya que según parece, lo que nos has mandado es un sistema de una ecuación con una incógnita.
Confírmanos si te piden resolver el sistema usando logaritmos y te orientamos para que resuelvas el ejercicio.
Saludos!
hola. nesesito un poco de ayuda
log (28-x^2) + log (x)=4
{x+1} {x+1}
Hola Mathias,
No entiendo a qué se refiere el {x+1}. ¿cómo va integrado en el ejercicio del logaritmo? Nos puedes poner el enunciado completo de lo que te piden para poder ayudarte a resolverlo?
Saludos!
Hola buenas tardes.
Una ayuda por favor, tengo (log en base (2401/16) de (1/128) )elevado a la —1 : log en base 512 de (49/4) tengo que resolver usando propiedades pero no me sale.
Hola Pablo,
Si lo tienes elevado a la -1, puedes empezar a resolver el ejercicio usando la propiedad del logaritmo de una potencia.
Si trabajar con fracciones te dificulta los cálculos, siempre puedes convertirlo a número decimal.
Saludos!
Escriba estas ecuaciones en forma logarítmica:
a) x= 2^9
b) x= 3^5
ayúdenme por favor
Hola Luis,
Te resolvemos la primera ya que la segunda se haría exactamente igual. Sólo tienes que aplicar la fórmula de logaritmo que es la siguiente:
logab = x ↔ b = ax
Tú partes del enunciado x=29 que es la segunda parte de la fórmula del logaritmo y por lo tanto:
b = x
a = 2
x = 9
Ahora sólo tienes que sustituir en forma logarítmica de la ecuación:
log2x = 9
¿Te atreves a hacer la siguiente?
Saludos!
hola, necesitaria el resultado de los sig:
log(4x-1)-(logx-2)=log5
2logx-log(x+6)=0
log(x+1)-logx=1
gracias
Hola Oriana,
Te hacemos uno de los ejemplos que nos mandas ya que nuestra labor no es la de resolver ejercicios. Los otros dos se harían igual.
2logx – log(x+6) = 0
Lo que hacemos es reordenar los elementos a ambos lados de la igualdad y nos queda:
2logx = log(x+6)
Por las propiedades de los logaritmos, tenemos que:
logx2 = log(x+6)
Ahora podemos despejar los logaritmos y nos queda la ecuación:
x2 = x + 6
Reagrupamos todo y obtenemos la siguiente ecuación de segundo grado:
x2 – x – 6 = 0
Que al resolverla (aquí puedes hacerlo: https://www.calculadoraconversor.com/calculadora-ecuacion-segundo-grado/) nos sale que x = 3 y x = -2
Si tienes alguna duda concreta para los otros dos nos dices.
Saludos!
Hola buenas tardes,no sabría como hacer este ejercicio de logaritmo es Log(3x^2+ 16x) – Log(x+36) – 1= 0 osea se que tengo que dividir 3x^2+ 16x/x+36 pero después no se como seguir
Hola,
Tienes que eliminar el denominador de la ecuación mediante factorización y resolver la ecuación de tercer grado que te quedará.
Saludos!
Podrían ayudarme con logartimos de fracciones?
Log2 1/4 ( log en base 2 de 1/4)
Hola Ana,
Qué problema tienes exactamente? Ten en cuenta que el logaritmo de una fracción puedes expresarlo como Log2(0,25).
Lo único que hemos hecho es pasar la fracción a decimal y resolverlo.
Saludos!
Como puedo resolver log 32/log2 gracias.
Hola Armando, sólo tienes que aplicar las propiedades de los logaritmos para resolver ese ejercicio.
log32 / log2 = log32 – log2
Simplemente tienes que resolver cada logaritmo de forma individual, efectuar la resta y obtendrás el resultado que buscas.
Saludos!
ayuda por favor
Log (x-2)•x=8
Hola Jc,
Tu ejercicio es bastante sencillo. Lo primero que hacemos es dejar a un lado de la ecuación sólo el logaritmo:
Log (x-2) = 8/x
Ahora usamos las propiedades de los logaritmos para resolver:
(x-2) = 10(8/x)
Y ahora simplemente debes despejar el valor de X.
Saludos!
Hola, necesito alguna pista para poder resolver el siguiente ejercicio, ya que no consigo encontrar las reglas que debo de aplicar, agradecería enormemente algún tipo de pista, el ejercicio es el siguiente:
simplificar la siguiente expresión: x elevado a 1 partido por el logaritmo en base a de x
lo maximo que consigo es reducirlo a 1 partido de x elevado al logaritmo en base a de x
muchas gracias.
Hola como resuelvo esta ecuacion
Log con base X (3x+10)=2
?????
buenas tardes, tengo una duda a ver si me pueden ayudar, a mi hijo le han dicho que necesita una calculadora cientifica para calcular todo tipo de logaritmos , la que el lleva es una caso fx 3800 p,
mi pregunta es que modelos hacen esa funcion que le piden?????
y le valdria alguno de estos dos modelos que le digo, casio fx82super fraction o la texas instruments TI 30 STAT???????
MUCHAS GRACIAS!!!
Hola Nuria,
Con la calculadora casio que comentas puede calcular cualquier tipo de logaritmos sin problema.
Saludos!