La función exponencial es la contraria a la del logaritmo neperiano y matemáticamente se denota bajo la fórmula f(x)=ex. Teniendo en cuenta esta premisa, la función exponencial se utiliza en numerosos problemas matemáticos.
Con nuestra calculadora de la función exponencial, podrás calcular esta operación en el que está involucrado el número de Euler.
Contenido de este artículo
Propiedades de la función exponencial
La función exponencial tiene una serie de reglas que debemos conocer y que os detallamos a continuación:
- exp (x + y) = exp(x) · exp(y)
- exp (x - y) = exp(x) / exp(y)
- exp (-x) = 1/exp(x)
- exp (0) = 1
Teniendo en cuenta estas cuatro propiedades para las funciones exponenciales, podrás simplificar mucho tus cálculos cuando te encuentres con derivadas, integrales u otras operaciones matemáticas en las que estén presentes.
Crecimiento exponencial ¿Qué significa?
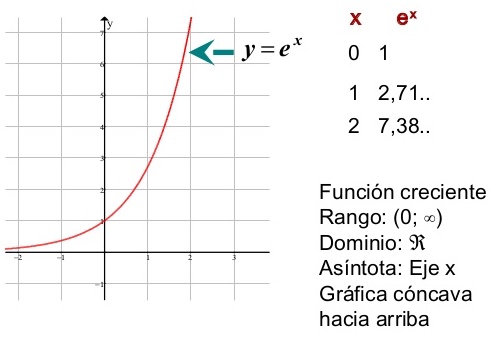
Para entender bien qué significa un crecimiento exponencial hemos creído conveniente acompañar la explicación de la gráfica de la función ex para que quede bien claro.
Si te fijas, para valores menores negativos de la función exponencial, el valor de y apenas aumenta. Sin embargo, para valores positivos de x, el crecimiento de y se dispara hasta tender a infinito.
Otra cosa que puedes apreciar de la función exponencial es que nunca nos va a dar como resultado un número negativo, por lo tanto su rango es de cero hasta infinito y, por lo tanto, se trata de una función creciente.
Derivada de la función exponencial
La derivada de una función exponencial tiene como resultado a la propia función exponencial.
Integral de la función exponencial
Si tenemos en cuenta que la integral es considerada como la antiderivada, entonces podemos tener ya una pista de cuál será la integral de las exponenciales.
Al igual que sucede con las derivadas, la integral de una función exponencial es la propia función más la constante C.
Valor del número de Euler
Como ya hemos dicho antes, las funciones exponenciales se caracterizan porque el número e o número de Euler está involucrado pero, ¿cuál es su valor?
Número e = 2,71828182...
El número e tiene infinitos números decimales ya que se trata de un número racional, exactamente igual que el número PI por lo que de cara a trabajar con el número de Euler, lo mejor es que cojamos una cantidad de tres o cuatro decimales para añadir la precisión más que suficiente para ejercicios del colegio o universidad.
Cómo calcular una exponencial en Excel
Está claro que Excel también es otra herramienta más para calcular el valor de una exponencial. Para ello debes hacer uso de esta fórmula:
=EXP()
y entre paréntesis escribir el valor del exponente que se aplica sobre la base e.
EXP en calculadora científica
En el caso de las calculadoras científicas, depende un poco del modelo que tengas. En el caso de muchas Casio científicas tendrás que localizar la tecla 'ln' ya que su función secundaria será la que usaremos para calcular una exponencial.
Por ejemplo, si queremos calcular e4, debemos marcar la siguiente combinación de teclas:
SHIFT → LN → 4 → ) → =
El paréntesis lo hemos usado porque el modelo de calculadora científica que estamos usando nos abre uno al pulsar el botón para calcular exponenciales así que hay que cerrarlo para que al pulsar la tecla de igual no nos de un error la operación.
Si te ha quedado alguna de cómo resolver una potencia con el número de Euler de base, déjanos un comentario e intentaremos responderte lo antes posible para ayudarte.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.