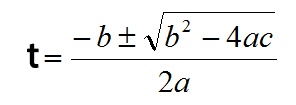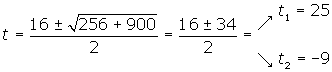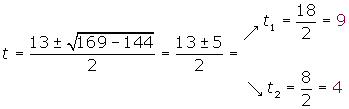¿Necesitas resolver ecuaciones bicuadradas? Usa nuestra calculadora online y obtén las cuatro soluciones de la ecuación de forma inmediata.
Recuerda que una ecuación bicuadrada son ecuaciones de cuarto grado (no confundir con las ecuaciones de segundo grado) sin ningún término de grado impar. Es decir, tienen este aspecto:
ax4 + bx2 + c = 0
Para usar nuestra calculadora calculadora de ecuaciones bicuadradas sólo tienes que escribir los valores de a, b y c y pulsar el botón de calcular para obtener el resultado.
Contenido de este artículo
Cómo resolver ecuaciones bicuadradas
Ya hemos visto que una ecuación bicuadrada es de la forma:
ax4 + bx2 + c = 0
Para resolverla, lo que vamos a hacer es transformarla en una ecuación de segundo grado que sí sabemos resolver. Para ello, haremos un cambio de variable en el que:
x2 = t
Por lo tanto, si hacemos el cambio de variable en la ecuación bicuadrada, pasaremos a tener una ecuación de segundo grado de la forma:
at2 + bt + c = 0
Las ecuaciones de segundo grado ya sabemos resolverla (pulsa en el link que te acabamos de dejar si no sabes cómo se hace) así que de ella nos saldrán dos soluciones:
t = t1
t = t2
Pero como hicimos un cambio de variable en el que x2 = t, tendremos que sacar las cuatro soluciones de la ecuación bicuadrada resolviendo las siguientes raíces cuadradas:
x1 = +√ t1
x2 = -√ t1
x3 = +√ t2
x4 = -√ t2
Transformando una raíz bicuadrada en una ecuación de segundo grado facilitamos mucho su cálculo.
Ejercicios de ecuaciones bicuadradas resueltos
Para poner en práctica la teoría que acabamos de ver con ejercicios de ecuaciones bicuadradas, vamos a resolver la siguiente ecuación:
x4 − 16x2 − 225 = 0
Hacemos el cambio de variable x2 = t y la transformamos en la siguiente ecuación de segundo grado:
t2 - 16t - 225 = 0
Para resolverla, aplicaremos la fórmula general que nos permite obtener las soluciones de una ecuación de segundo grado:
Haciendo las sustituciones en la fórmula anterior y resolviendo, nos queda que:
Ahora que ya sabemos las soluciones, deshacemos el cambio de variable que hemos hecho al principio del artículo:
x1 = +√ t1 = +√ 25 = 5
x2 = -√ t1 = -√ 25 = -5
x3 = +√ t2 = +√ -9
x4 = -√ t2 = -√ -9
La tercera y cuarta solución no la resolvemos ya que no existen números reales de la raíz cuadrada de -9 (sólo podemos hacer la raíz cuadrada de números positivos). Dejando esto indicado en el ejercicio es suficiente.
Ejemplo de ecuaciones bicuadradas
Por si el ejercicio anterior de ecuaciones bicuadradas no ha quedado muy claro, vamos a ver otro más en el que nos piden resolver:
x4 − 13x2 + 36 = 0
Realizamos el cambio de variable x2 = t para transformarla en una ecuación de segundo grado:
t2 - 13t + 36 = 0
Y la resolvemos:
Por último, deshacemos el cambio de variable y sacamos las cuatro soluciones de la ecuación bicuadrada inicial:
x1 = +√ t1 = +√ 9 = 3
x2 = -√ t1 = -√ 9 = -3
x3 = +√ t2 = +√ 4 = 2
x4 = -√ t2 = -√ 4 = -2
Fácil, no? Si tienes alguna duda o quieres comprobar las soluciones, siempre puedes usar nuestra calculadora de ecuaciones bicuadradas o dejarnos un comentario y te ayudaremos a resolver el ejercicio.
¿Cuántas soluciones tiene una ecuación bicuadrada?
Aunque lo normal es que una ecuación bicuadrada tenga cuatro soluciones, puede darse el caso en el que tengan tres, dos, una única solución o incluso ninguna.
Por ejemplo:
- Si t1 = 0 ó t2 = 0, sólo tendremos una única solución al deshacer el cambio de variable y será x = 0
- Si t1 < 0 no tendremos ninguna solución como hemos visto en el primer ejemplo ya que no existen las raíces de un número negativo. Pasaría lo mismo si t2 < 0.
Si usas nuestra calculadora de ecuaciones bicuadradas y ves que en alguno de los campos de las soluciones no sale ningún dato es porque se ha dado alguna de las condiciones anteriores.
Resolver ecuaciones bicuadradas incompletas
A la hora de solucionar una ecuación bicuadrada incompleta, el procedimiento a utilizar es el mismo que en el primer punto de la teoría.
Es decir, hacemos el cambio de variable y como resultado obtendremos una ecuación de segundo grado incompleta que habrá que resolver siguiendo el procedimiento que te indicamos en la página del enlace que te acabamos de dejar.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.