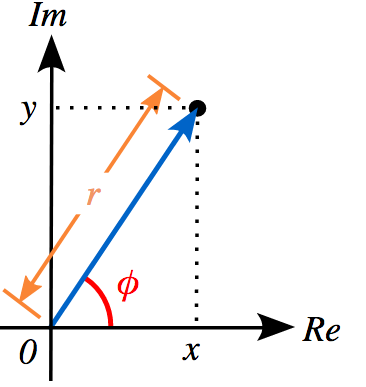
Calcular el módulo números complejos

Calcular el módulo de un número complejo (z = a + bi) es una operación sencilla pero que siempre solemos olvidar cómo se hace aunque gracias a nuestra calculadora ya no tendrás que recordar la fórmula.

También puedes usar la herramienta para sacar el valor absoluto de un complejo para comprobar que has resuelto los ejercicios correctamente.

Cómo se calcula el módulo de un número complejo en forma cartesiana

Un número complejo en forma cartesiana o binómica es del tipo z = a + bi y calculamos su módulo mediante la siguiente fórmula:

|z| = √(a² + b²)

Vamos a ver cómo se calcula el módulo de un número complejo en forma cartesiana con un ejercicio resuelto en el que nos dan z = 2 + 3i

|z| = √(2² + 3²) = √(4 + 9) = √13 = 3,6055

Cómo calcular el módulo de un número complejo en forma polar

Si tenemos el número complejo en forma polar , el módulo ya está implícito en su expresión y no tenemos que hacer ningún cálculo.

Un número complejo en forma polar es de la forma z = r_α, siendo r el valor del módulo y α el argumento.

Por ejemplo, si nos dan el número complejo 3_120º, el módulo es 3.

Calcular el módulo de un complejo en Excel

Si tienes Excel instalado en tu ordenador, puedes usarlo para calcular el módulo de cualquier número complejo con una sencilla fórmula.

Si quieres probar cómo se hace, abre una nueva hoja de cálculo y escribe la siguiente función en una celda vacía:

=IM.ABS("5+3i")

Eso nos devolverá el valor absoluto o el módulo del complejo 5 + 3i.

Lo que tienes que hacer es modificar la fórmula para sacar el valor absoluto del número complejo que quieras.

Propiedades del módulo de un número complejo

A continuación tienes algunas de las propiedades del módulo de un número complejo:

1. La multiplicación de un número complejo por su conjugado nos da como resultado el módulo del número complejo elevado al cuadrado.
2. El módulo de un número complejo siempre es mayor o igual a cero, por lo tanto, nunca puede ser negativo. Será mayor que cero si el número es diferente de cero y será cero solo cuando el número sea cero. Esto queda expresado matemáticamente así:

|z| = 0 si, y sólo si, z = 0.

3. El módulo de un número complejo es igual al módulo del conjugado del número complejo. Es decir:

|z| = |z'|

4. El módulo del producto de dos números complejos es igual al producto de los módulos de los números complejos de forma individual, algo que matemáticamente se expresa así:

|z₁z₂| = |z₁| |z₂|

5. La propiedad anterior también se aplica a la división, es decir, el módulo del cociente de 2 números complejos es igual al cociente de los módulos de los números complejos.

|z_{1 /} z₂| = |z₁| / |z₂|

6. La parte real y la parte imaginaria de un número complejo es menor o igual al módulo del número complejo.

|Re(z)| ≤ |z|

|Im(z)| ≤ |z|

7. La desigualdad triangular nos dice que el módulo de la suma de dos números complejos es menor o igual a la suma de los módulos de los números complejos. Esto también sucede con la resta.

|z1 + z2| ≤ |z1| - |z2|

|z1 -  z2| ≤ |z1| - |z2|

Calculadora del módulo de un número complejo

Para facilitarte el cálculo del módulo de un número complejo en forma binómica (recuerda que en polar no hay que hacer ninguna operación), hemos creado una calculadora para que obtengas el resultado automáticamente.

Su funcionamiento es muy sencillo y sólo tienes que escribir los valores a y b del número complejo del cual quieres obtener su número.

Cuando lo hayas escrito, pulsa el botón calcular y obtendrás la respuesta. Sin duda te será muy útil para ahorrar tiempo en operaciones o para comprobar si los ejercicios resueltos que has hecho están bien calculados.

Nacho

Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.