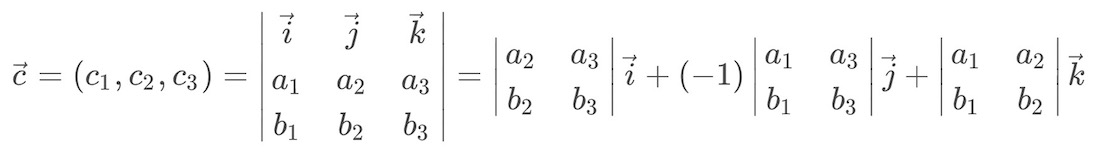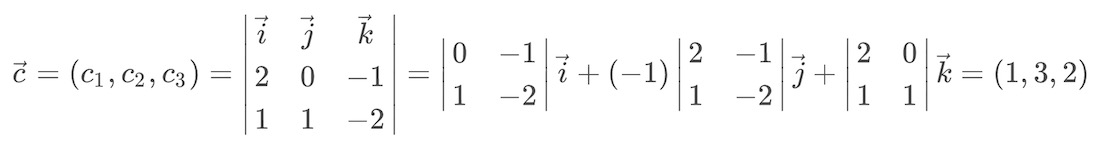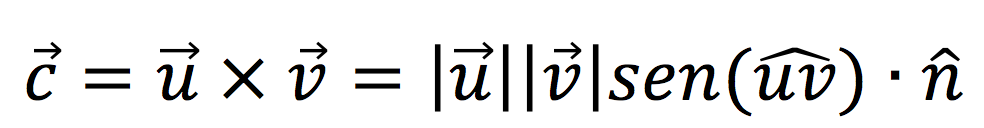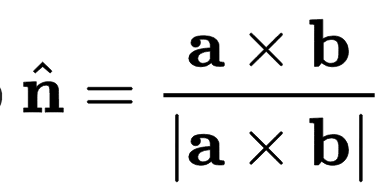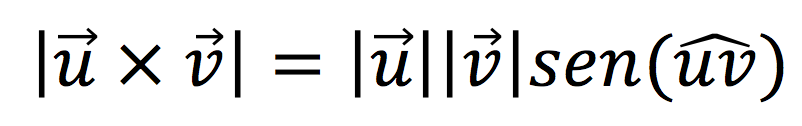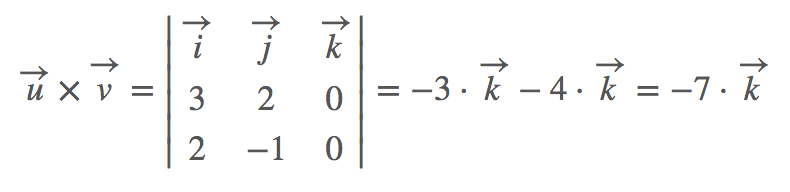¿No sabes cómo calcular el producto vectorial de dos vectores? Usa nuestra calculadora online y averigua automáticamente el resultado, sin hacer operaciones.
Sólo tienes que introducir las componentes i, j y k de los dos vectores y pulsar el botón de calcular para obtener su producto vectorial. Por ejemplo, si te dan el vector = (1, 2, 3) y
= (4, 5, 6), los valores de cada una de sus componentes son los que debes escribir en la herramienta. Si no sabes cómo se calcula el producto vectorial, sigue leyendo y te lo explicamos.
Contenido de este artículo
¿Qué es el producto vectorial?
El producto vectorial de dos vectores nos da como resultado otro vector con:
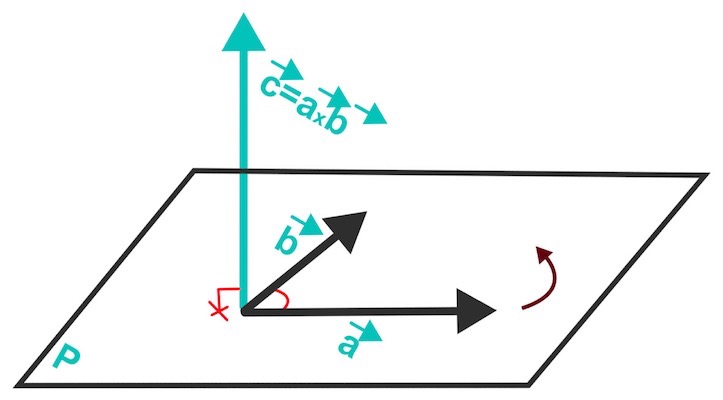
- Dirección perpendicular a los dos vectores
- Sentido en base a la regla del sacacorchos o de la mano derecha.
¿Qué dice la regla de la mano derecha? La regla de la mano derecha o del sacacorchos nos dice el sentido que tendrá el vector según el movimiento de un sacacorchos (o destornillador, tornillo...etc).
En el caso de la figura que tenéis encima de estas líneas podéis ver que si hacemos girar el sacacorchos hacia la izquierda (sentido antihorario), el sacacorchos sube hacia arriba y, por lo tanto, esa será la dirección del vector "c" resultante.
Es muy importante que no lo confundas el vectorial con el producto escalar.
Cómo se hace el producto vectorial de dos vectores
Para resolver el producto vectorial de dos vectores = (a1, a2, a3) y
= (b1, b2, b3), tenemos que aplicar la siguiente fórmula que nos dará las componentes del vector "c":
Básicamente hay que escribir en un determinante de 3x3 y descomponerlo en tres determinantes 2x2 para cada componente i, j, k.
No hace falta que recuerdes los elementos del determinante asociados a cada elemento ya que se pueden deducir de forma sencilla. Simplemente tienes que calcular el determinante adjunto, es decir, tienes que eliminar la fila y columna en la que se encuentra cada elemento i, j, k de tal forma que con los elementos restantes formas un determinante 2x2. Aquí te enseñamos cómo resolver un determinante de una matriz 2x2.
Por ejemplo, vamos a ver un ejercicio resuelto en el que nos piden calcular el producto vectorial de los vectores = (2, 0, -1) y
= (1, 1, -2):
Como resultado del producto vectorial, tenemos este vector:
Existe un segundo método para calcular el producto vectorial de dos vectores a partir de la siguiente fórmula matemática:
El método consiste en multiplicar sus módulos por el seno del ángulo que forman y el vector unitario "n" que es ortogonal a los vectores y cuyo sentido y dirección se rige por la regla de la mano derecha.
Si no sabes cómo se hace, aquí te explicamos cómo calcular el módulo de un vector.
Módulo del producto vectorial
Para calcular el módulo del producto vectorial de dos vectores tienes que usar esta fórmula:
En este caso, el resultado será un número escalar que nos representa la longitud que tendrá el segmento del vector resultante.
Producto vectorial de dos vectores en R2
Si nos piden calcular el producto vectorial de dos vectores en R2, el proceso a seguir es exactamente igual que en R3. Simplemente tendremos que completar con un 0 la componente del vector que nos falte.
Por ejemplo, vamos a calcular el producto vectorial de los vectores en R2 = (3, 2) y
= (2, -1).
Como puedes ver, no tenemos componente "k", así que los elementos a3 y b3 serán cero. Teniendo en cuenta este detalle, resolvemos el ejercicio y nos queda lo siguiente:
Triple producto vectorial
El triple producto vectorial (también conocido como doble producto vectorial) consiste en multiplicar vectorialmente dos vectores y con el resultado obtenido realizar otro producto vectorial con el vector que nos falta. Por ejemplo:
A × (B × C) = B (A · C) – C (A · B)
Al multiplicar los vectores B x C generamos un vector que posteriormente tenemos que multiplicar vectorialmente por A. El resultado sería un vector contenido en el plano definido por B y C.
Como el doble producto vectorial tiene propiedad anticonmutativa, también podemos expresarlo así:
A × (B × C) = - C x (A x B)
Para terminar, destacar que el triple producto no tiene propiedad asociativa.
Propiedades del producto vectorial
A continuación tienes las propiedades del producto vectorial que aún no han sido mencionadas:
- Anticonmutativa: a x b = - (b x a)
- a · (a x b) = 0
- Si a x b = 0 siendo a≠0 y b≠0, esto quiere decir que los vectores son paralelos y por eso su producto vectorial es cero.
- (a + b) x c = a x c + b x c
- a x (b x c) + c x (a x b) + b x (c x a) = 0 según la identidad de Jacobi
Aplicaciones del producto vectorial
Son muchas las aplicaciones que tenemos para el producto vectorial en el mundo de las matemáticas, física o astronomía.
Algunas de las que siempre se suelen poner como ejemplo y que nos permiten calcular el área y volumen de algunas figuras geométricas como el triángulo o un paralelogramo.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.