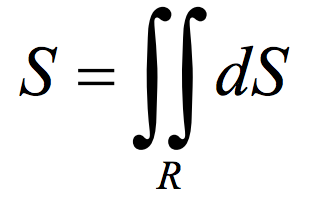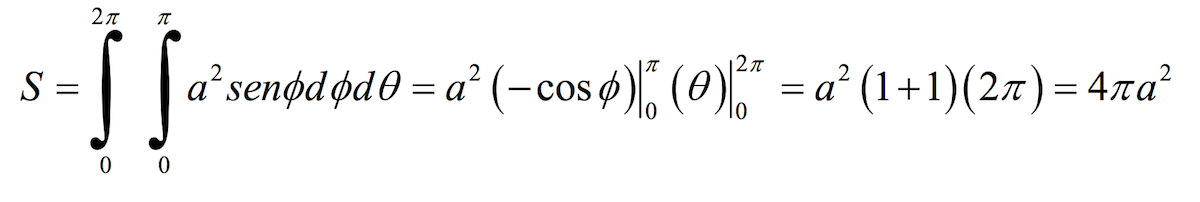Si necesitas calcular el área de una esfera online, gracias a nuestra calculadora puedes conseguirlo con sólo introducir el valor del radio de esta figura.
Para calcular el área de una esfera de forma manual sólo tienes que multiplicar por cuatro el radio al cuadrado de la esfera y todo ello por el número PI, así sacarás el valor de su superficie.
Si lo que quieres es saber el volumen de esta figura, puedes hacerlo con nuestra herramienta para calcular el volumen de una esfera.
Contenido de este artículo
¿Cuál es el área de una esfera?
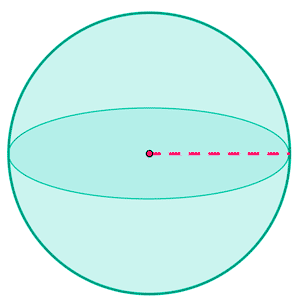
Si no tienes claro cuál es el área de una figura con volumen como la esfera, en la representación que tenéis encima de estas líneas podéis ver una zona con sombreado más oscuro que representa la superficie que ocupa dicha esfera.
El área de una esfera se define como cuatro veces su radio al cuadrado por π. En el siguiente punto veremos cómo se calcula a partir de su fórmula.
Cómo calcular el área de una esfera
Para calcular el área de una esfera tenemos que aplicar la siguiente fórmula matemática:
Área esfera = 4πr2
dónde r será la medida del radio.
Ejercicio resuelto para hallar el área de una esfera
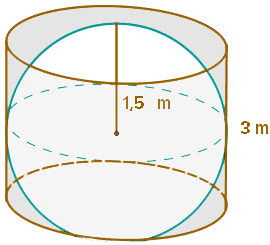
Por ejemplo, vamos a calcular cuál es el área de una esfera que está dentro de un cilindro de 3 metros de altura.
Como se puede ver en la figura, los tres metros corresponden al diámetro de la esfera pero nosotros necesitamos el radio que es la mitad de ese valor, es decir, 1,5 metros.
Ahora aplicamos la fórmula y nos queda que:
Área esfera = 4π1,52 = 9π = 28,27 m2
Como puedes ver, la resolución del problema es sencillo y la única dificultad radica en acordarse de cuál es la fórmula para calcular el área de la esfera.
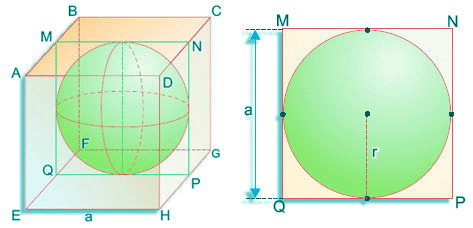
Área de una esfera inscrita en un cubo
Si tenemos una esfera inscrita en un cubo, se trata del mismo caso que hemos visto antes con el cilindro. Sólo tenemos que tener en cuenta que la medida del lado del cubo será el diámetro de la esfera.
Por ejemplo, si nos piden calcular el área de una esfera inscrita en un cubo de lado 10cm, lo primero que haremos será calcular el radio r:
radio = lado del cubo / 2 = 5 cm
Ahora aplicamos la fórmula para sacar la superficie de una esfera:
A = 4π52 = 100π = 314,15 cm2
Área de una esfera con integrales
Para calcular la superficie de una esfera mediante integrales dobles o de superficie usaremos la siguiente expresión:
Para entender la demostración, lo haremos sobre un ejemplo en el que vamos a hallar el área de una esfera dada por la ecuación x2 + y2 + z2 = a2
La esfera es una figura que puede parametrizarse con las siguientes ecuaciones paramétricas:
- x = a senΦ cosθ
- y = a senΦ senθ, con θ ∈ (0, 2π),Φ ∈ (0, π)
- z = a cos Φ
que definen el vector de posición de esta forma:
R (Φ,θ) = (a senΦ cosθ, a senΦ senθ , a cos Φ)
El diferencial de superficie en este tipo de superficies parametrizadas está definido como:
dS = ||RΦ x Rθ || dΦdθ
Hacemos las derivadas parciales y tenemos:
RΦ = (a cosΦ cosθ, a cosΦ senθ , -a senΦ)
Rθ = (-a senΦ senθ, a senΦ cosθ, 0)
Ahora resolvemos el producto vectorial y calculamos su magnitud:
Finalmente nos queda que el área de la esfera calculado por integrales dobles o de superficie es:
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.