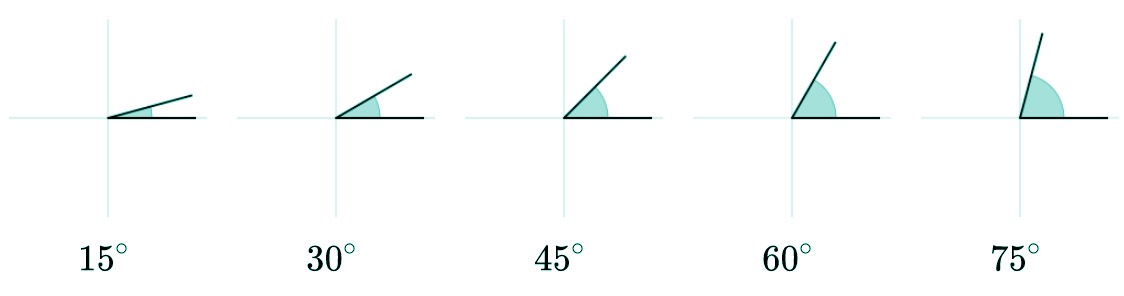¿Necesitas saber qué tipo de ángulo es uno en concreto y calcular su suplementario o complementario? Usa nuestra calculadora online y obtendrás el resultado que buscas de forma inmediata. Sólo tienes que escribir la amplitud del ángulo en grados y pulsar el botón de calcular para conocer su clasificación.
Si quieres aprender más sobre los tipos de ángulos que existen en base a su medida, su suma, su posición u otros criterios, sigue leyendo porque aquí encontrarás toda la información que buscas.
Contenido de este artículo
Clases de ángulos según su medida
La primera clasificación de ángulos que vamos a ver está basada en su tamaño. A continuación tenéis una tabla que resume los tipos de ángulos en base a su amplitud que podemos medir en grados o en radianes. Si necesitamos más precisión, también podemos convertir el grado en grados, minutos y segundos.
| Tipo de ángulo | Medida |
|---|---|
| Nulo | 0º |
| Agudo | Menos de 90º |
| Recto | 90º |
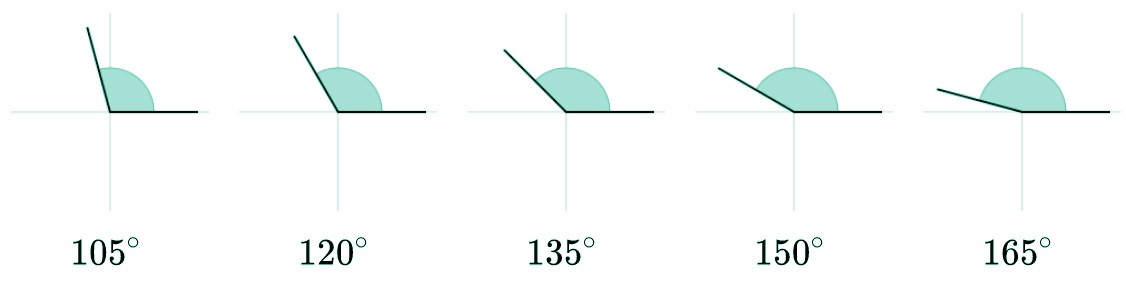
| Obtuso | Más de 90º y menos de 180º |
| Llano | 180º |
| Completo | 360º |
| Convexo | Entre 0º y 180º |
| Cóncavo | Entre 180º y 360º |
Por si te ha quedado alguna duda, a continuación veremos cada tipo de ángulo según su medida con algo más de detalle.
Ángulo nulo
El ángulo nulo es aquel que vale 0º y está formado por dos semirrectas coincidentes, algo que provoca que su apertura sea nula.
Ángulo agudo
El ángulo agudo es aquel que tiene una amplitud entre 0º y 90º o entre 0 y π/2 si lo expresamos en radianes.
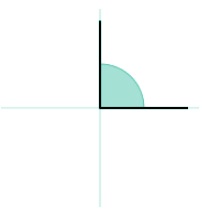
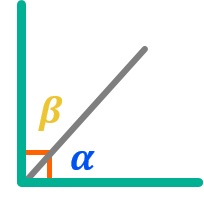
Ángulo recto
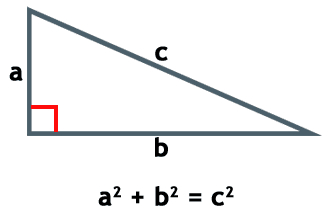
Llamamos ángulo recto a aquel que tiene exactamente 90 grados o π/2 radiantes. Es un ángulo muy conocido en trigonometría ya que está presente en el Teorema de Pitágoras, por lo que trabajarás con él frecuentemente.
Cuando nos encontramos con un ángulo recto, se suele dibujar una especie de caja en la esquina (la tienes representada en color rojo en la imagen superior). Dicha caja sólo se dibuja con los ángulos que tienen 90º por lo que es una forma de identificarlos rápidamente.
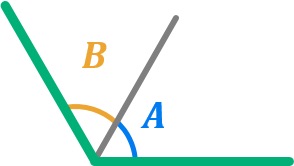
Ángulo obtuso
Se denomina ángulo obtuso a aquel que tiene una amplitud superior a 90º pero menor a 180º. Si hablamos en radianes, su medida es superior a π/2 radiantes pero menor que π radianes.
Ángulo llano
De los ángulos llanos no hay mucho que decir ya que miden exactamente 180º o π radianes. En algunos sitios se denomina al ángulo llano como extendido pero es una denominación poco frecuente.
Ángulo completo
Definimos como ángulo completo aquel cuya amplitud es de 360º o 2π radianes, en definitiva, una vuelta completa.
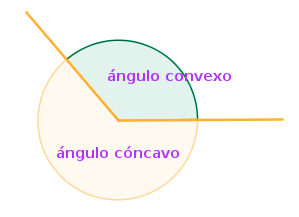
Ángulo cóncavo y convexo
Siempre existen dudas sobre los ángulos cóncavos y convexos ya que no solemos acordarnos de cual es cada uno.
- Ángulo convexo: mide entre 0º y 180º (entre 0 y π radianes)
- Ángulo cóncavo: mide más de de 180º pero menos de 360º.
Como puedes ver, ambos se clasifican en función de su medida con respecto al ángulo llano (180º). Si es menor que éste será convexo por el tipo de curvatura mientras que si es mayor será cóncavo.
Tipos de ángulos según su suma
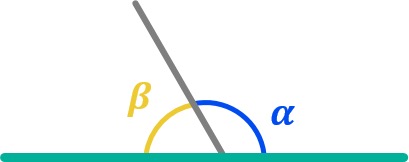
La segunda clasificación de ángulos que vamos a ver está basada en función de la suma de dos ángulos. Dependiendo del valor que nos de dicha suma, tendremos ángulos suplementarios o complementarios:
Ángulos suplementarios
Son dos ángulos que al sumarlos nos dan 180º. Vamos a ver varios ejemplos:
- El ángulo suplementario de 30º es 150º.
- El ángulo suplementario de 123 grados es 57º.
- El suplementario de 45º es 135º
De lo anterior podemos deducir que dos ángulos son suplementarios si:
- Los dos miden 90º o son ángulos rectos
- Uno es obtuso (mide más de 90º) y el otro ángulo es agudo (tiene menos de 90º)
¿Cómo encontramos el ángulo suplementario de otro del que conocemos su valor? Simplemente tenemos que resolver la siguiente fórmula:
Ángulo suplementario = 180º - α
Siendo α la amplitud en grados del ángulo que conocemos.
Ángulos complementarios
Dos ángulos complementarios son aquellos que al sumarlos nos dan 90º. Por ejemplo:
- El ángulo complementario de 30º es 60º
- El complementario de 35º es 55º
- El ángulo complementario de 120º es -30º
La fórmula para encontrar el ángulo complementario de otro es la siguiente:
Ángulo complementario = 90º - α
Tipos de ángulos según su posición
Ángulos adyacentes
Los ángulos adyacentes con aquellos que cumplen las siguientes características:
- Tienen un lado y el vértice en común
- El otro lado se encuentra en la misma recta
Por los requisitos anteriores, los ángulos adyacentes son siempre ángulos suplementarios (suman 180º) y consecutivos.
Ángulos consecutivos
Los ángulos consecutivos tienen las siguientes características:
- Tienen un lado y el vértice en común
- El otro lado no se encuentra en la misma recta, por lo que no son ángulos suplementarios (no suman 180 grados)
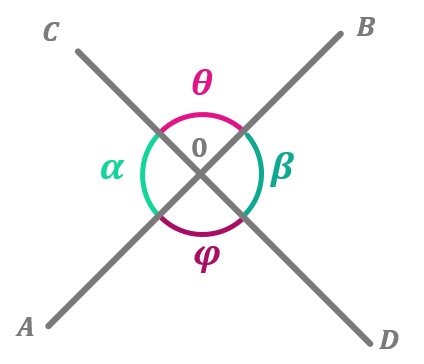
Ángulos opuestos por el vértice
Los ángulos opuestos por el vértice son aquellos que tienen sus lados situados sobre las mismas rectas y éstas se cortan en el vértice que tienen en común. De esta forma
- α = β
- θ = φ
En este tipo de ángulos tienes que saber que:
α + β + θ + φ = 360º
Pero si tenemos en cuenta las igualdades que hemos visto antes, la ecuación podemos simplificarla así:
2α + 2θ = 360º
2 (α + θ) = 360º
α + θ = 180º
Gracias a la demostración anterior podemos ver que ambos ángulos son suplementarios y podemos hallar el valor de alguno de ellos si conocemos el del otro.
Ángulos entre paralelas y una recta transversal
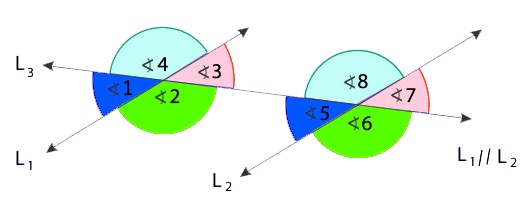
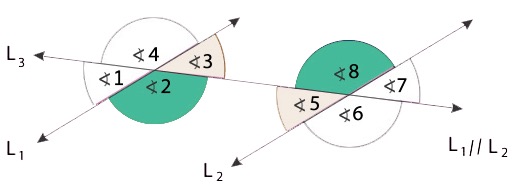
Existe una tercera clasificación de ángulos que tenemos cuando existen dos rectas paralelas y otra recta transversal que las atraviesa, formando un total de 8 ángulos que podemos clasificar de diferente manera en función de su posición.
Ángulos correspondientes
Llamamos ángulos correspondientes a aquellos que tienen la misma posición con respecto a la recta transversal, lo que además hace que tengan la misma medida o amplitud.
En el caso de la imagen, serían ángulos congruentes aquellos correspondientes los pares:
- 1 y 5
- 3 y 7
- 4 y 8
- 2 y 6
Ángulos alternos internos
Los ángulos alternos internos son aquellos que se sitúan dentro de la región comprendida entre las rectas paralelas. De nuevo, se generan varios pares de ángulos que son iguales:
- 2 y 8
- 3 y 5
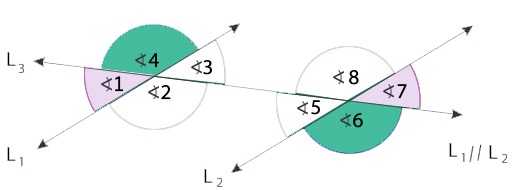
Ángulos alternos externos
Los ángulos alternos externos son aquellos que se encuentran en la parte exterior de la región comprendida entre las rectas que son paralelas. En este caso, serán iguales los siguientes ángulos:
- 4 y 6
- 1 y 7
Esto se debe al Teorema de los ángulos alternos externos y por el cual podemos ver que:
∠1 + ∠4 = 180º
∠6 + ∠7 = 180º
Igualamos ambas ecuaciones y nos queda que:
∠1 + ∠4 = ∠6 + ∠7
Si resolvemos, podemos ver que los ángulos 4 y 6 son iguales, algo que también sucede entre los ángulos 1 y 7.
Si te ha quedado alguna duda sobre los tipos de ángulos que existen o conoces más clasificaciones que quieres que añadamos, déjanos un comentario y te ayudaremos lo antes posible.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.