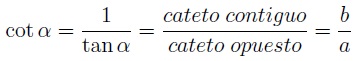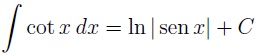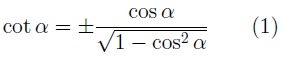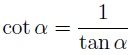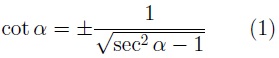¿Quieres calcular la cotangente online? Con nuestra calculadora podrás hacerlo para cualquier ángulo, ya esté en en grados o en radianes. Tras pulsar el botón de calcular obtendrás el valor de la cotg.
Si además quieres aprender más aspectos sobre esta función trigonométrica inversa, en el artículo te enseñaremos todo lo que debes saber en relación a ella.
Contenido de este artículo
Fórmula de la cotangente
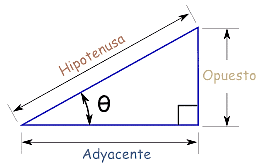
¿Qué es la cotangente de un ángulo? Es una función de trigonometría que se calcula dividiendo el cateto adyacente entre el cateto opuesto. También se define como el inverso de la tangente.
En base a lo anterior, nos queda la siguiente fórmula para calcular la cotangente:
Tabla de valores de la cotangente
A continuación encontrarás una tabla con los valores habituales que toma la cotangente para ángulos típicos de todos los cuadrantes:
| Grados | Radianes | Cotangente |
|---|---|---|
| 0º | 0 | ±∞ |
| 30º | π/6 | 1,7320 |
| 45º | π/4 | 1 |
| 60º | π/3 | 0,5773 |
| 90º | π/2 | 0 |
| 135º | 3π/4 | -1 |
| 180º | π | ±∞ |
| 225º | 5π/4 | 1 |
| 270º | 3π/2 | 0 |
| 315º | 7π/4 | -1 |
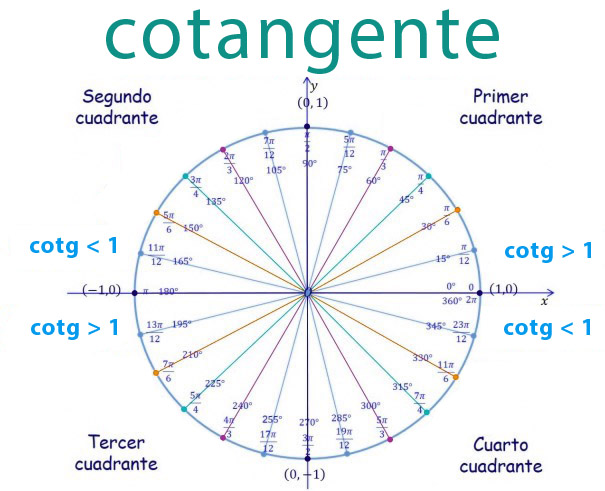
Si analizamos los resultados de la tabla anterior, podemos ver que el valor de la cotangente será:
- Negativo si el ángulo se encuentra en el 2º o 4º cuadrante
- Positivo si el ángulo está en el primer o tercer cuadrante
Esto que os acabamos de decir lo podéis ver representado en el siguiente gráfico:
Cotangente de 0
¿Cuál es la cotangente de 0? Si tratas de resolver esta respuesta con la calculadora, verás que obtienes como resultado un error. ¿Por qué? Vamos a verlo:
Antes hemos dicho que la cotangente es la inversa de la tangente, por lo tanto:
tan 0º = 0
Ahora calculamos el valor de la cotg:
cotg = 1 / tan 0º = 1 / 0 = ±∞
Recuerda que algo entre cero es igual a infinito pero la calculadora lo trata como una indeterminación y por eso nos devuelve un error en el cálculo.
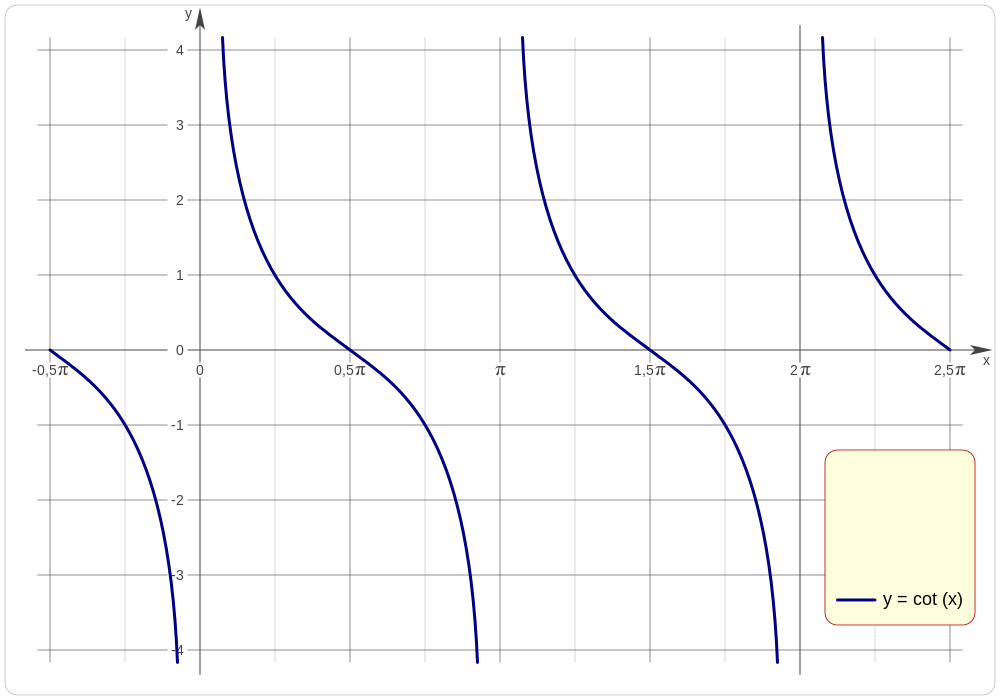
¿Por qué la cotangente de 0 es infinito? Para verlo con más claridad, vamos a fijarnos en la gráfica de la función cotangente:
Si nos fijamos en el valor 0 del eje de las x, podemos ver que la función no está definida pero dependiendo de si nos aproximamos por la izquierda o por la derecha, su valor tiende a -∞ o +∞ respectivamente. Podemos decir que existe una asíntota.
Esto también ocurre en valores que sean múltiplos de nπ, siendo n un número entero.
Características
La cotangente tiene como característica principal que su dominio está formado por todos los números reales (ℝ) a excepción de aquellos ángulos que sean múltiplos de nπ ya que, tal y como hemos visto en el apartado anterior, en esos valores la función no está definida y tiende a infinito.
Su recorrido es en todo ℝ.
Derivada de la cotangente
La derivada de la cotangente es igual a -1 menos la cotangente al cuadrado de x. Esto lo podemos expresar de forma matemática de la siguiente manera:
f(x) = cotgx → f'(x) = -csc2x = -1 - cotg2x
Integral de la cotangente
Si lo que queremos es calcular la integral de la cotangente, entonces usaremos esta fórmula:
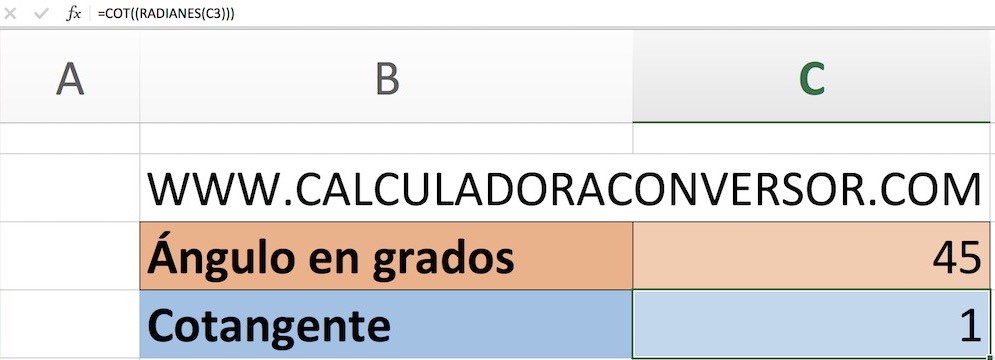
Cómo calcular la cotangente en Excel
En Excel también podemos calcular la cotangente de forma sencilla con una función específica que incorpora el programa de hojas de cálculo de Microsoft. Para hacer la prueba, abre una hoja de cálculo nueva y escribe en una celda vacía la siguiente función:
Si el ángulo está en grados:
=COT((RADIANES(ángulo)))
Si el ángulo está en radianes:
=COT(ángulo)
Sólo tienes que cambiar la palabra "ángulo" de la fórmula por la cantidad de grados o radianes que quieras. Por ejemplo, si queremos calcular la cotangente de 90 pondremos así la fórmula:
=COT((RADIANES(90)))
Cotangente en función de otras razones trigonométricas
Dado que todas las funciones de trigonometría están relacionadas unas con otras, es posible expresar la cotangente en función de cualquiera de ellas. A continuación tenéis todas las fórmulas:
En función del seno:
En función del coseno:
En función de la tangente: esta fórmula es la fórmula más sencilla de toda ya que como vimos al principio del post, por definición la cotangente es igual a la inversa de la tangente.
En función de la secante:
En función de la cosecante:
Todas las fórmulas que tienen la anotación (1) a su derecha significa que dependiendo del cuadrante al que pertenezca el ángulo, el resultado será positivo o negativo.
Calcular cotangente en calculadora
Si quieres calcular la cotangente de un ángulo con la calculadora, debes saber que salvo que tengas un modelo de calculadora científica o programable de gama alta, no encontrarás ningún botón para resolver esta operación. Sin embargo, existe un método dividido en varios pasos que nos permitirá hacerlo.
Como hemos visto al inicio del post, la cotangente es igual al inverso de la tangente. Por eso, dividiremos el cálculo de la operación en los siguientes pasos:
- Calcular la tangente del ángulo
- Calcular la inversa del resultado obtenido en el paso anterior.
Por ejemplo, vamos a ver cuál es la cotangente de 30 con la calculadora. Para ello, lo primero que haremos es calcular la tangente del ángulo pulsando las siguientes teclas:
TAN > 30 > =
Con el resultado en pantalla, a continuación tenemos que localizar la tecla que tiene el símbolo x-1 y pulsamos el botón igual (=) para resolver la operación, de esta manera obtendremos el inverso que es el valor de la cotg.
Si hemos hecho los pasos correctamente, en la pantalla de la calculadora deberá aparecer un resultado igual a 1,73. En caso de que hayas obtenido otra cosa, revisa los pasos y si tienes configurada la calculadora para funcionar en grados y no en radianes.
En el caso de que tengas cualquier tipo de duda o problema relacionado con la cotangente, déjanos un comentario y te ayudaremos a resolver tus inquietudes.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.