Calcula la tangente de cualquier ángulo con nuestra herramienta. Introduce el ángulo en grados o radianes y presiona el botón de calcular para obtener su tangente.
También tenemos disponibles calculadoras para calcular el seno y el coseno por lo que si te son de ayuda, a continuación tienes los enlaces que te llevarán a cada una de ellas.
Contenido de este artículo
Cómo calcular la tangente
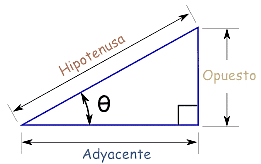
Para calcular la tangente en un triángulo rectángulo, simplemente tenemos que hacer la división del cateto opuesto dividido entre el contiguo, es decir:
tan θ = cateto opuesto / cateto adyacente
Por ejemplo, vamos a imaginar que tenemos un triángulo rectángulo cuyo cateto opuesto mide 3 centímetros y el contiguo tiene una longitud de 7 cm. Con esos datos, el seno se calcularía así:
tan θ = 3 cm / 7 cm = 0,428
Si sabemos el valor del seno y el coseno, otra forma de calcular el valor de la tangente es aplicar la siguiente fórmula matemática:
tan θ = sen θ / cos θ
Ambas formas de calcular el valor de la tangente son válidas pero utilizaremos una u otra en función de los datos de partida que tengamos.
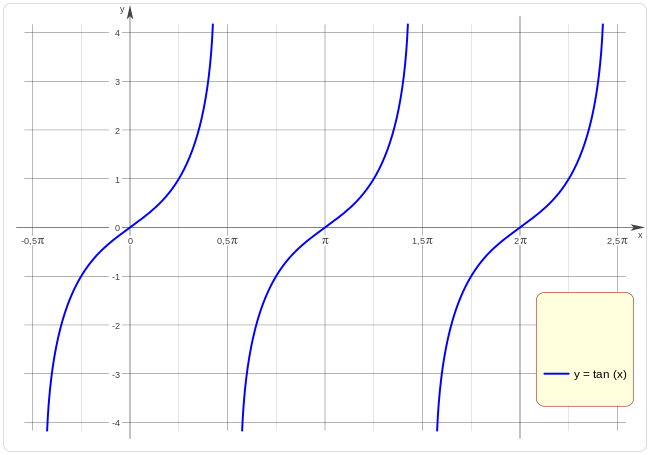
Representación gráfica de la función tangente
En la gráfica anterior puedes ver la forma que tiene esta función trigonométrica.
Tabla de la función tangente
Trabajar con la función tangente es más cómodo si disponemos de una tabla que recoja la tangente de los ángulos más habituales en los problemas de mátemáticas. Ten en cuenta que la tangente es el seno entre el coseno, por eso, para los ángulos de 90 grados y 270 grados nos encontramos con que la función trigonométrica no está definida y tiende a infinito.
| Grados | Radianes | Tangente |
|---|---|---|
| 0º | 0 | 0 |
| 30º | π/6 | 0.577 |
| 45º | π/4 | 1 |
| 60º | π/3 | 1.732 |
| 90º | π/2 | Infinito |
| 180º | π | 0 |
| 270º | 3π/2 | Infinito |
| 360º | 2π | 0 |
La tangente de 30 es igual a 0,577. Esta es una de las dudas más frecuentes que tenéis y que más nos preguntáis a diario.
Derivada de la tangente
Si quieres calcular la derivada de la tangente de x, lo más recomendable es que escribas la equivalencia de la tangente en términos del seno y coseno de x ya que son derivadas que sí conocemos. Resolvemos y nos quedaría que la derivada de la tangente de x es:
Si en lugar de tener la variable x tenemos una función, entonces la derivada de la tangente de una función se complica un poco más:
En este segundo caso, la derivada de la TAN de una función será igual a la derivada de esa función por 1 más la tangente al cuadrado de esa función.
Integral de la tangente
A continuación puedes ver cuál es la integral de la tangente de x:
∫ tan x dx = -ln|cos x| + C
Cómo funciona la calculadora de tangente
Nuestra calculadora de tangente online tiene un funcionamiento muy sencillo. Lo único que debes hacer es introducir el ángulo en la casilla correspondiente y seleccionar la unidad, ya sea en grados o en radianes si lo prefieres.
Por ejemplo, si quieres calcular la tangente de 30 grados, sólo tendrás que escribir el número y dejar las unidades como están ya que por defecto nuestra calculadora de tangente trabaja con grados.
Ese es el funcionamiento básico, ya te dijimos al principio que es muy fácil de usar.
Cómo calcular la tangente en Excel
Si quieres crear tu propia calculadora para hallar la tangente, puedes hacerte una usando Excel. El programa de Microsoft tiene una función dedicada a resolver esta función de trigonometría que funciona de la siguiente forma.
Abre una hoja de cálculo nueva y en una celda vacía escribe la siguiente función para sacar la tangente de un ángulo:
=TAN()
Entre los paréntesis tienes que escribir el ángulo en radianes ya que por defecto ese es el argumento de entrada.
Si quieres hacer el cálculo de la tangente en Excel con un ángulo en grados, entonces debes escribir la función de esta forma:
=TAN(RADIANES(90))
En el ejemplo que te acabamos de dejar hemos calculado la tangente de 90 grados pero puedes sustituir ese número por el ángulo en grados que tú quieras.
Si tienes alguna duda en relación a esta función de trigonometría tan usada, escríbenos un comentario y te ayudaremos. Y si te ha gustado nuestro trabajo también nos lo puedes dejar :)
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.