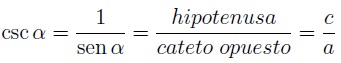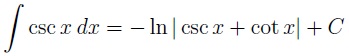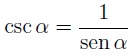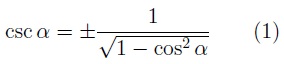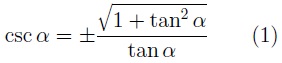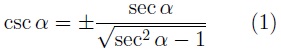¿Tienes que calcular la cosecante online de un ángulo? Usa nuestra herramienta y podrás hacerlo tanto en grados o en radianes. Sólo tienes que escribir el valor del ángulo, seleccionar la unidad en la que está y pulsar el botón de calcular para obtener el valor de la cosec(x).
Si quieres saber más sobre esta razón trigonométrica inversa, cómo se calcula, sus propiedades y más, sigue leyendo.
Contenido de este artículo
Fórmula de la cosecante
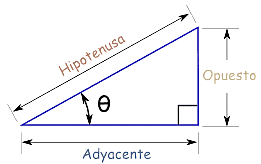
¿Qué es la cosecante? Se trata de una razón trigonométrica inversa al seno y que podemos expresar matemáticamente mediante la siguiente fórmula:
Como puedes ver, tenemos múltiples maneras de calcular la cosecante de un ángulo. Por un lado podemos hallar el inverso del seno y, por otro, dividir el valor de la hipotenusa entre el cateto opuesto.
Tabla de valores de la cosecante
Para conocer un poco más de la cosecante, a continuación vamos a ver algunos de sus valores típicos para ángulos habituales mediante esta tabla:
| Grados | Radianes | Cosecante |
|---|---|---|
| 0º | 0 | ±∞ |
| 30º | π/6 | 2 |
| 45º | π/4 | 1,4144 |
| 60º | π/3 | 1,1547 |
| 90º | π/2 | 1 |
| 135º | 3π/4 | 1,4144 |
| 180º | π | ±∞ |
| 225º | 5π/4 | -1,4144 |
| 270º | 3π/2 | -1 |
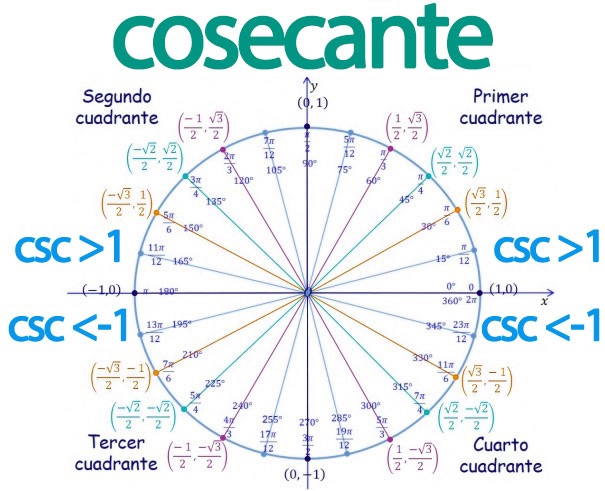
Haciendo este breve repaso por todos los cuadrantes de un círculo, podemos ver como la cosecante es:
- Negativa en el tercer y cuarto cuadrante
- Positiva en el primer y segundo cuadrante
Esto queda representado de forma más clara en el siguiente gráfico:
Gráfica de la cosecante
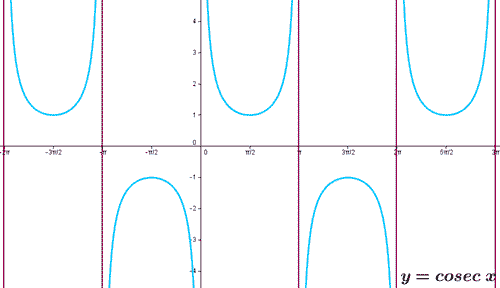
Ahora que ya sabemos los valores que adquiere la cosecante de x a lo largo del periodo 2π radianes o 360º, podemos dibujar la gráfica de la función, quedándonos su representación de la siguiente forma:
Como ya adelantábamos, se puede ver la periodicidad cada 2π radianes o 360 grados.
Características
Además de ser una función periódica, la cosecante tiene las siguientes características:
- Dominio: todo ℝ (los números reales), exceptuando los valores que sean múltiplo de a·π. En esos valores, la función tiene asíntotas verticales y tiende a ±∞ dependiendo del cuadrante en el que nos encontremos.
- El recorrido se encuentra definido en el intervalo (-∞, -1] U (1, +∞)
- No corta al eje de abscisas o al de ordenadas en ningún punto.
- Al ser simétrica con respecto al origen, se trata de una función par.
- No se encuentra acotada
Derivada de la cosecante
¿Cuál es la derivada de la cosecante de x? Es igual a la menos cosecante de x por la cotangente de x. Expresado matemáticamente quedaría así:
f(x) = cosecx → f'(x) = -cosecx · cotanx
Si en lugar de x tenemos la cosecante de una función, tendremos que calcular también su derivada y, por lo tanto, nos quedará así:
f(u) = cosecu → f'(u) = - u' cosecu · cotanu
Integral de la cosecante
Si lo que quieres es calcular la integral de esta función trigonométrica inversa, esta es la fórmula que debes usar:
Cómo calcular la cosecante en Excel
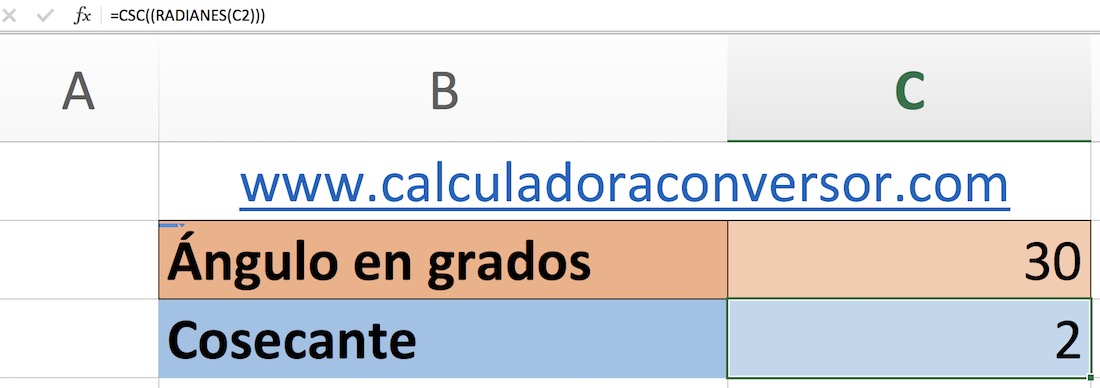
En el caso de que necesites calcular la cosecante de un ángulo en Excel, puedes hacerlo de forma sencilla independientemente de que el ángulo esté en grados o en radianes.
Sólo tienes que escribir en una celda vacía alguna de las siguientes funciones y sustituir la palabra "ángulo" por la cantidad de grados o radianes que necesites para el cálculo.
Ángulo en grados:
=CSC((RADIANES(ángulo)))
Ángulo en radianes
=CSC(ángulo)
Por ejemplo, si queremos calcular la cosecante de 60 grados, la fórmula que escribiremos en Excel será la siguiente:
=CSC((RADIANES(60)))
Cosecante en función de otras razones trigonométricas
Como todas las funciones trigonométricas están relacionadas entre sí, podemos expresar la fórmula para calcular la cosecante en función del seno, del coseno o cualquier otra. Veamos cada caso de forma individual:
En función del seno: Este es el caso más sencillo ya que como vimos al principio del post, la cosecante se devine como la inversa del seno.
En función del coseno:
En función de la tangente:
En función de la secante:
En función de la cotangente:
Todas las fórmulas que tienen la indicación (1) significa que el resultado será positivo o negativo en función del cuadrante del ángulo α.
Calcular cosecante en calculadora
Salvo que tengas una calculadora científica o programable muy avanzada, no encontrarás una tecla específica para poder calcular la cosecante de forma directa. Por eso, tenemos que hacer el cálculo en dos pasos.
- Calcular el seno del ángulo
- Calcular el inverso del resultado obtenido en el paso anterior.
Por ejemplo, si queremos calcular la cosecante de 30, haremos lo siguiente. En primer lugar, obtenemos el seno pulsando la siguiente combinación de teclas:
SEN > 30 > =
Con el resultado que hemos obtenido, a continuación pulsamos la tecla que tiene grabado x-1 y pulsamos el botón de igual (=) para resolver la operación. Aquí lo que hemos hecho es calcular el inverso.
Si todo ha ido bien, la calculadora te mostrará en pantalla un resultado igual a 2. Si no te sale eso, comprueba que has seguido los pasos correctamente y que tienes la calculadora configurada para trabajar en grados en lugar de radianes.
Si tienes cualquier tipo de problema o duda sobre el cálculo de la cosecante de un ángulo, déjanos un comentario y te ayudaremos lo antes posible. De todas formas, te recomendamos siempre que uses nuestra calculadora online ya que es muy fácil de manejar y te evitarás cualquier tipo de error en los cálculos.
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.