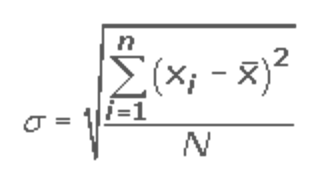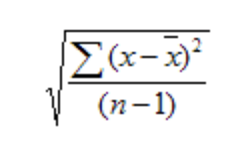¿Necesitas calcular la desviación típica de un conjunto de datos? Con nuestra calculadora puedes obtener la desviación estándar con sólo escribir cada cifra, separadas por un espacio o por una coma. Si vas a introducir números decimales, usa el punto '.' como separador decimal.
Cuando hayas escrito todos los números, pulsa el botón de calcular y automáticamente obtendrás el valor de la desviación así como otras medidas estadísticas como la varianza o la media.
Contenido de este artículo
Qué es la desviación típica
La desviación típica es una medida de dispersión que nos muestra la desviación que presentan los datos de la distribución en comparación con su media aritmética.
Esto nos ayuda a tener una visión más real de los datos para interpretarlos correctamente, algo que beneficia positivamente en la toma de decisiones.
La desviación estándar se usa mucho para ver cuánto se alejan los datos del promedio de la distribución.
La desviación típica también puede definirse como la raíz cuadrada de la varianza.
Fórmula de la desviación estándar
Para calcular la desviación estándar hay que aplicar la siguiente fórmula matemática:
Cómo calcular la desviación típica paso a paso
Si no entiendes bien cómo aplicar la fórmula de la desviación típica, a continuación tienes explicado paso a paso cómo calcularla. Sólo tienes que realizar los siguientes pasos:
- Calcular la media aritmética de los números del conjunto
- Restar a cada número la media obtenida y elevar el resultado al cuadrado
- Obtener la media de los resultados anteriores
- Realizar la raíz cuadrada al número resultante
Para que se entienda bien, vamos a ver un ejercicio resuelto de desviación típica.
Ejemplo de desviación estándar
Vamos a calcular la desviación estándar del conjunto de números [1, 3, 5, 7, 9].
Para ello, seguimos los pasos vistos en el punto anterior así que lo primero de todo es calcular su valor promedio:
(1 + 3 + 5 + 7 + 9) / 5 = 25 / 5 = 5
A continuación restamos a cada número del conjunto el valor de la media anterior. Posteriormente elevamos al cuadrado:
(1 - 5)2 = 16
(3 - 5)2 = 4
(5 - 5)2 = 0
(7 - 5)2 = 4
(9 - 5)2 = 16
El siguiente paso consiste en hallar la media de los valores anteriores:
(16 + 4 + 0 + 4 + 16) / 5 = 8
Por último, hacemos la raíz cuadrada del valor obtenido:
√8 = 2,828
Con esto ya hemos terminado.
Símbolo de la desviación típica
La desviación típica suele representarse con una letra s o con el símbolo σ.
Calcular la desviación típica en Excel
Para calcular la desviación típica en Excel existe una función que hace la operación automáticamente.
Para ello, sólo tienes que abrir el programa de hojas de cálculo de Microsoft y escribir cada número del conjunto en una celda independiente. Por ejemplo, vamos a imaginar que tenemos un conjunto formado por 10 valores que ocupa el rango de celdas A1:A10.
Para calcular la desviación típica en Excel escribimos la siguiente fórmula:
=DESVEST.P(A1:A5)
Lógicamente, tendrás que adaptar el rango de celdas de la fórmula a tu hoja de cálculo para abarcar las celdas en las que has escrito los datos del conjunto.
Es importante destacar que la fórmula anterior sirve para calcular la desviación estándar poblacional. Si lo que quiere es calcular la desviación típica muestral, entonces debes escribir esta otra fórmula:
=DESVESTA(A1:A5)
Desviación típica muestral
La desviación típica muestral se utiliza cuando suponemos que los datos del conjunto son solo una muestra de la población total.
En este caso, la fórmula matemática que usamos es esta:
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En esta web te ayudo a hacer cálculos y conversiones sencillas que con el paso de los años se nos ha olvidado cómo se hace. Si tienes dudas, déjame un comentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, escríbeme un mensaje.